Exponenciális eloszlású folyáshatárokkal végzett szimulációk
A legtöbb szimulációt olyan folyáshatárokkal végeztem, ahol azok értékeit exponenciális eloszlásból válaszottam. Ennek két oka volt:
- egyetlen paraméterrel jellemezhető, egyszerű eloszlás
- számítási költsége alacsony, így a program gyors maradhat
Vannak eredmények hatványfüggvény lecsengésű disztribúciók esetére, míg mások fél-Gauss eloszlást használtak. DDD vizsgálataink azt mutatták azonban, hogy Weibull-disztrubíciót lenne még érdemes vizsgálni, mely szerencsére szintén C++-os szabvány 2011 óta.
Különböző szimulációkat készítettem (1-1-ben gyakran több 1000 mérésre átlagolva), melyek egymástól általában csak 1 dologban különböztek. A kiinduló rendszer paraméterei:
- exponenciális eloszlású, paraméterű, tehát 5 várható értékű folyáshatár-eloszlás
- 1-es deformáció növekmény (DG)
- 2 hatvány méretű rendszerek, 128-tól kezdve
- 0 deformációjú kezdeti állapot
- 1 cella megfolyatása után újra meghatározom, hogy hol folyik meg leginkább a minta, tehát a deformációt a lavinában DG-nként növeltem
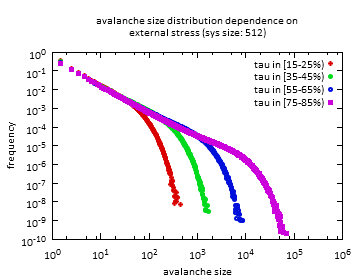
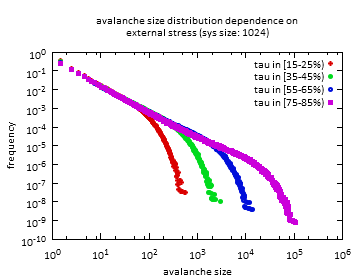
Feszültség függés
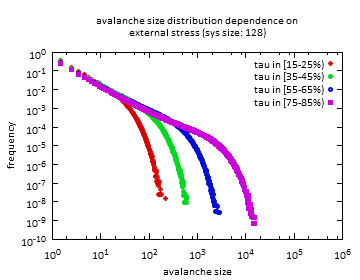
Korábbi kutatások megmutatták, hogy bármilyen külső feszültség esetén a lavinák méreteloszlása hatványfüggvény eloszlású egy adott mérettartományban, egy adott méret fölött (levágási méret) pedig exponenciálisan levág. A levágási méret értéke függ a külső feszültségtől, és egy adott értékhez közeledve a végtelenhez tart (a véges számú szimuláció esetén ez azt jelenti, hogy az összes, statisztikai mennyiségben előforduló, adott méretű lavinák mind hatványfüggvény eloszlást követnek, a méret nem vág le).
A lavinaméret-eloszlás feszültség függését vizsgálva a korábbi megállapításokat alátámasztjuk.
A lavina méretek egészek,
és a
tartományban vett lavinák vannak feltüntetve a 0.5-nél.
Forráskód a 4 ábrához.

Fig1-3: Lavinaméret eloszlás függése a külső feszültségtől.
Látható, hogy nagyobb feszültségnél a levágás értéke is nagyobb.
Közeledve a folyáshatárhoz, a levágás tolódik a nagyobb lavinák felé.
forráskód
Rendszerméret függés
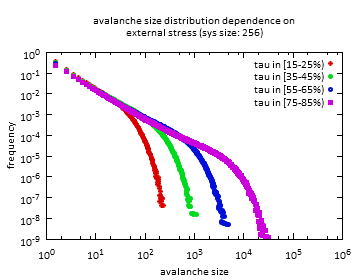
A lavinaméret-eloszlás rendszerméretfüggését vizsgálva azt tapasztalhatjuk, hogy nagyobb rendszereknél a levágási méret értéke is nő. Ez nem összeegyeztethető a diszlokáció-lavinákra eddig alkalmazott depinning-modellel, mely nem tartalmazott a rendszerméret-függő tagokat.
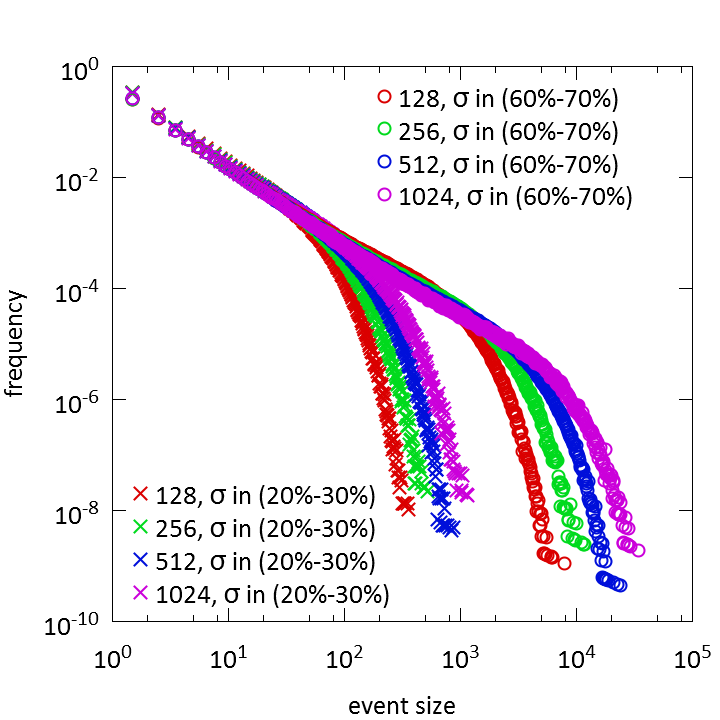
Fig2. Lavinaméret-eloszlás rendszerméretfüggése
két különböző feszültség tartományban.
Látható, hogy a rendszermérettel a levágás is nő.
forrás Fig3-mal együtt
Azonban a levágási méret nagy a vizsgált minta méretéhez képest, ami azt jelenti, hogy a deformációkat egy vonal mentén elrendezve az a mintát (1D mentén) többször körbeérné, vagyis a lavina feltehetőleg többször körbehalad a mintán, és önkölcsönhatás léphet fel, ezért érdemes volna nagyobb méretű rendszereket vizsgálni. Jellemző, hogy a levágási méret a megfolyási feszültség tizede környékén már összevethető a rendszer méretével, a felénél pedig már több tízszerese is lehet.
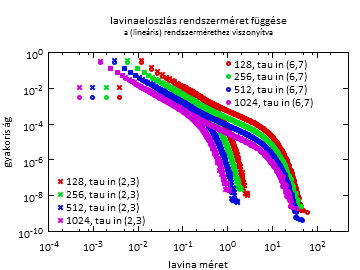
Fig3. Lavinaméret-eloszlás a rendszermérethez viszonyítva
különböző méretű rendszereknél.
A nagyobb rendszerknél a relatív-lavina méret kisebb.
Sajnos azonban
lassan csökken a relatív lavina méret,
így csak nagy számolás árán érhető el,
hogy
a lavinák a rendszerhez képest kicsik legyenek.
forrás Fig2-vel együtt
Nagyobb rendszerrel való vizsgálódás akkor jelent megoldást az aggodalmak enyhítésére, ha a levágási méret lassabban nő, mint a rendszer lineáris mérete. A mérések szerint ez teljesül, így érdemes még nagyobb rendszereket vizsgálni.
Feszültség-deformációs görbék
Vizsgáltam a kiátlagolt feszültség-deformációs görbéket, melyeket több 1000 mérésből átlagoltam össze. 1-1 szimulációnál az sejthető, hogy az exponenciális eloszlás által bevezetett feszültség skála (az eloszlás lambda paramétere) kétszeresénél az addigi össz deformációt lényegesen meghaladó, végtelen nagynak tekinthető lavinák keletkeztek.
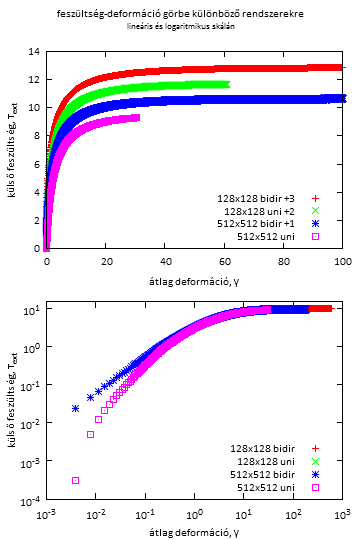
Fig4a: több ezer mérésre kiátlagolt feszültség-deformációs görbék.
Az egyirányú és kétirányú rendszerekre nincs számottevő különbség.
forrás
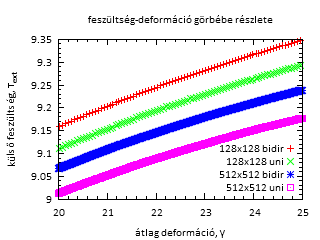
de a valódi viszonyuk az ott ábrázoltnak megfelelő.
A kiátlagolt görbéken az látható, hogy a görbe ellaposodik, egy konstans értékhez tart, a minta megfolyik. A logaritmikus ábrázoláson az látható, hogy nem hatványfüggvény szerint tart ehhez a konstans értékhez.
A belső feszültségeloszlásról készült hisztogram a különböző deformációs értékek mellett. Érdemes volna ugyanakkor megvizsgálni a belső feszültségek folyáshatárhoz képesti értékének eloszlását is.
Deformáció-növekmény megválasztása
Konklúzió: a deformáció megválasztásának módja nem befolyásolja lényegesen a statisztikai paramétereket, ugyanakkor alapvető fonrosságú a negatív lavinák méretének szabályozásában. Az a deformációs érték megválasztási mód tűnik helyesnek, amikor a deformációt úgy választjuk meg, hogy a helyi feszültség 0 legyen a deformációt követően.
Leírás: a szimulációban ha egy cellában a külső dipólok és a külső feszültség feszültségértékeének összege meghaladja a lokális folyáshatár értékét, azaz , akkor a deformációnak a cellában nőnie kell. A deformáció növekmény megválasztását többféleképp is elvégezhetjük.
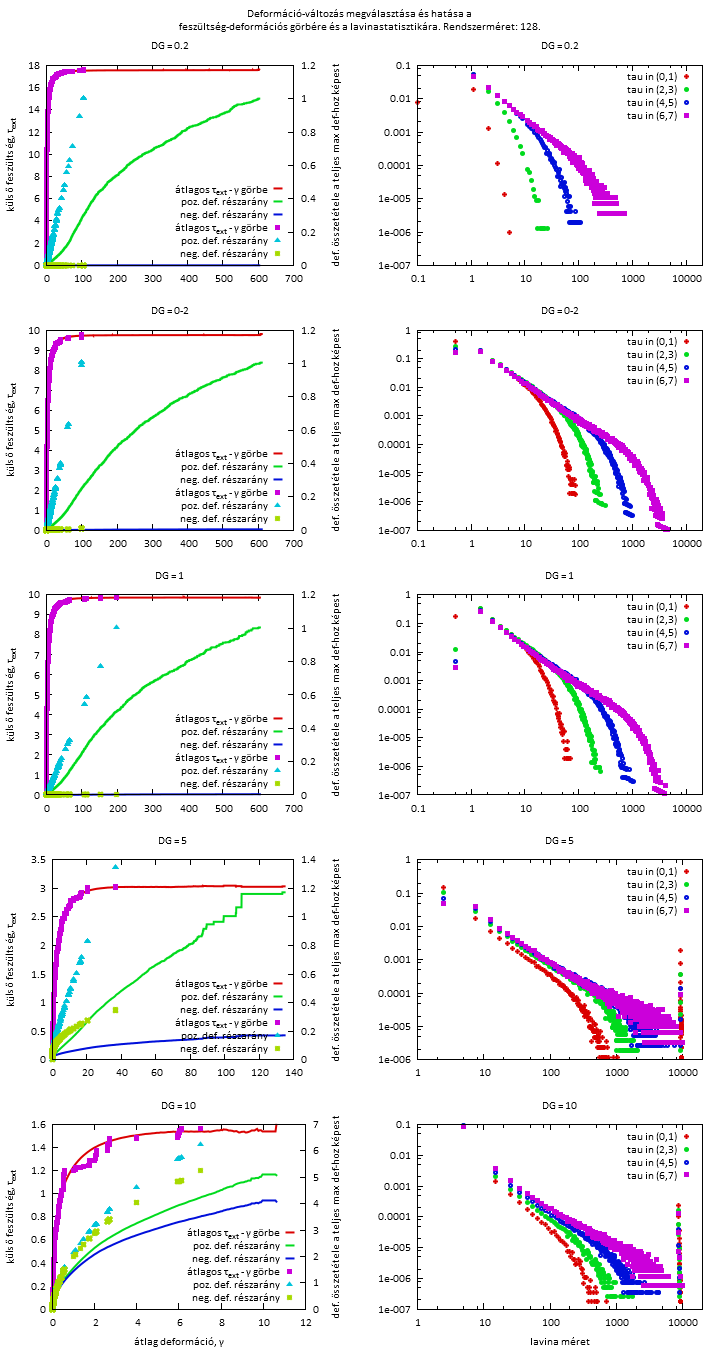
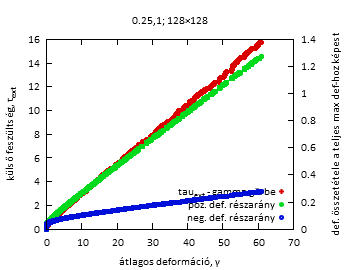
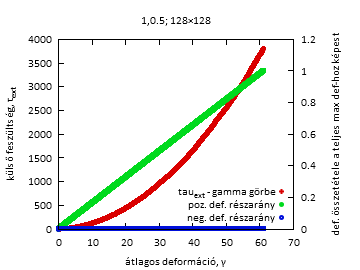
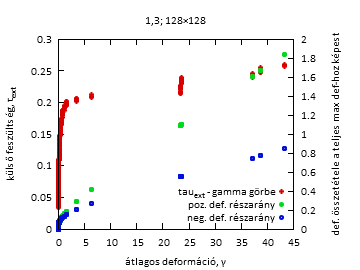
Fig4a. Feszültség-deformációs görbe és összetétele pozitív és negatív deformációkból
1-1 konkrét szimulációnál, és kiátlagolva, valamint a lavinastatisztika. DG: cella deformációjának változása a cella megfolyása során.
forrás
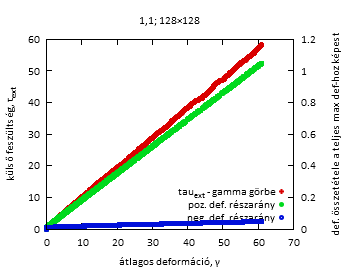
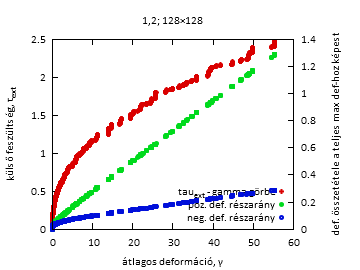
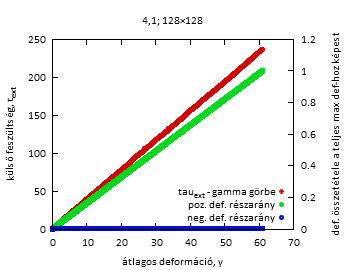
A deformáció-növekmény kis értéke esetén egy konkrét feszültség-deformációs görbén láthatóan kisebbek a lavinák, és kevés a negatív lavina, míg nagy deformáció-növekmény értékek esetén jóval nagyobbak a lavinák, és a negatív lavinák aránya is jóval nagyobb.
A lavinastatisztikában a rendszerméret környékén a görbe "megvastagodik", azaz egyik lavinaméretnél kisebb, a rákövetkezőnél nagyobb a gyakoriság. Ezt a véges rendszerméret okozhatja: a lavinák gyakran 1 vonalban gerjesztődnek, és egy sor gerjesztés után nagyobb eséllyel állnak meg. Vagy ha nem állnak meg épp, akkor már inkább folytatják...
Fig4b. Feszültség-deformációs görbe és összetétele pozitív és negatív deformációkból
1-1 konkrét szimulációnál, és kiátlagolva, valamint a lavinastatisztika (50 szimulációra átlagolva, 128-as rendszerméret). DG: cella deformációjának változásának megválasztásához használt eloszlás paramétere.
forrás
Különböző hatótávolságú deformációk
A rácsban keltett deformációk diszlokáció dipólok, melyek feszültségterének lecsengése -es. A dipól kristályos anyagban jól értelmezhető, azonban általánosítható amorf anyagokra is, illetve vizsgálható, hogyan viselkedik a rendszer, ha nem a dipólnak megfelelő feszültségeteret használjuk.
Vizsgáltam a különböző hatótávolságú rácshibákkal a rendszert, ezek:
- extrém rövid hatótávolságú (csak a szomszédos pontokkal kölcsönható), local
- -es lecsengésű, de a diszlokáció dipólokkal ellentétben (szögben) izotróp, isotropic
- extrém nagy hatótávolságú (mindegyik ponttal egyformán kölcsönható), meanfield

Fig6c: Extrém hosszú hatótávolságú kölcsönhatás.
Feszültségterek ábrázolása a 128x128-as rendszerekre. A 128. sor és oszlop is meg van jelenítve.
forrás mind 3 ábrához
Érdemes összevetni a lavinastatisztikákat a dipólteres feszültségtérrel.



80-as lavina méret fölött logaritmikusan, 101.25% széles binekkel végzett osztályozás.
Érdemes megjegyezni, hogy a 0 méretű lavinából kevesebb van, mint az 1 méretűből.
A normálás az összes előforduló lavinát tekintve végeztem,
mivel azonban egyesek extrém nagyok,
s nem vesznek részt a hisztogramban,
ezért az ábrázolt eloszlás nem 1-re normált elméletben, gyakorlatban viszont igen.
Forrás mind a 3
ábrához
Lavinastatisztikák
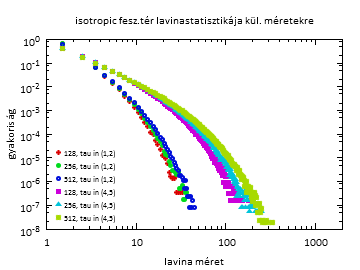
Fig8a: izotróp feszültségtér esetén a statisztika.
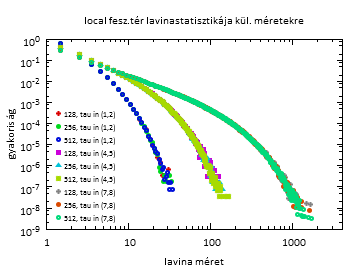
Fig8b: local feszültségtér esetén a statisztika.
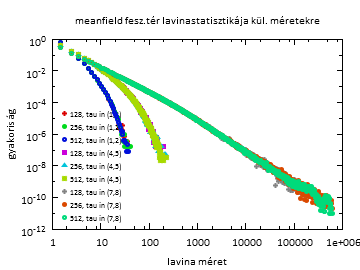
Fig8c: meanfield feszültségtér esetén a statisztika.
A local és a meanfield esetén nem nő a rendszermérettel a levágás. Meglepő, mert meanfield esetén nőnie kéne.
Forrás az ábrákhoz
Azt láthatjuk, hogy a meanfield esetén nem nőtt a levágás a rendszermérettel. A magyarázat az lehet, hogy a nagyobb renszerméret esetén a meanfield térnél az origóban vett értéket tartottuk állandónak, a távoliakat kisebbnek választottuk. A releváns program részlet:
for(int i=0; i<N; ++i)
for(int j=0; j<N; ++j)
{
//Mean field
sprintf(fname, "meanfield_N%d.dat", N);
if(i!=0 || j!=0)
x[i][j] = 2.0/(N*N-1);
if(i!=0 || j!=0)
s += x[i][j];
}
x[0][0] = -s;
Újabb futtatásokat végezve, melyben a távoli értékét a feszültségtérnek állandónak vettük, és a 0-ben vett értékét módosítottuk úgy, hogy az átlaga 0 legyen, a jelenség ...
Fig8d: a feszültségtér rendszermérettel való más skálázásával a lavinastatisztika rendszerméretfüggését is változtathatjuk.
Forrás az ábrákhoz
Az új térnél használt kód releváns része:
for(int i=0; i<N; ++i)
for(int j=0; j<N; ++j)
{
//Mean field const
sprintf(fname, "meanfield_const_N%d.dat", N);
if(i!=0 || j!=0)
x[i][j] = 2.0/(128*128-1);
if(i!=0 || j!=0)
s += x[i][j];
}
x[0][0] = -s;
Korrelációk vizsgálata
Deformációs és lokális feszültség térképek autokorrelációi
Legelőször az av_max_DGamma szimulációk eredményeit értékeltem ki, melyet Péter be is mutatott egy konferencián. Azonban mint kiderült, az autokorrelációt hibásan számoltam ki: a Fourier transzformáció után nem abszolút érték négyzetet, hanem abszolút értéket számoltam. A hibás eredmény szerint kicsi x-ekre , mind a deformációra, mint a lokális feszültségre.
A helyes autokorrelációs számítások eredménye alapján az látható, hogy a összefüggés továbbra is igaznak bizonyul kicsi x-ekre. Leellenőriztem, hogy az új kód pontosan csak abban különbözik a régitől, hogy abszolút érték négyzetet számol ott, ahol kell.
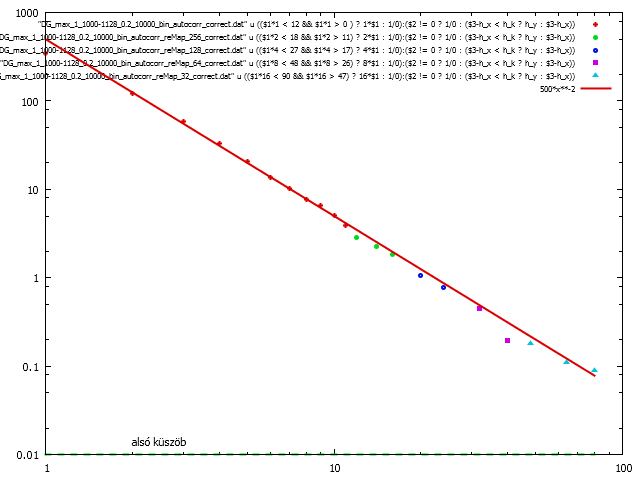
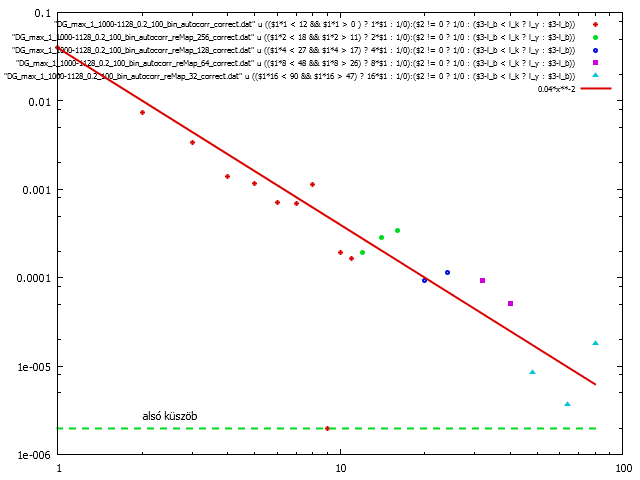
reMap nélküli eredmény (nagy, kicsi)
forrás (nagy, kicsi)
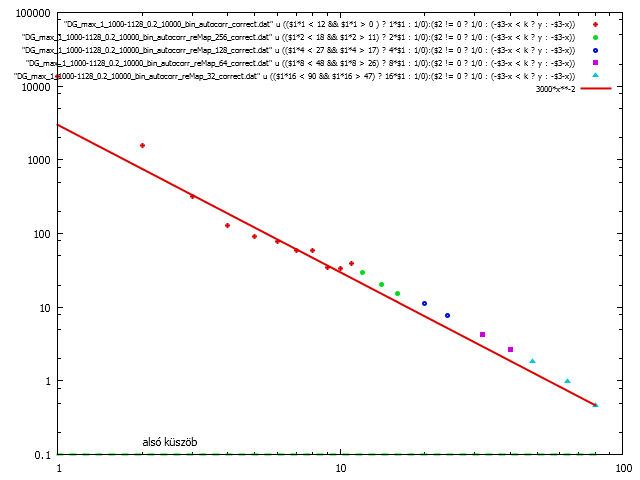

Lokális feszültség térképek autokorrelációja 512-es rendszerméret esetén a av_max_DGamma szimulációnál 10000-es és 100-as deformáció értéknél (a helyes összefüggéssel számolva). Látható, hogy itt is igaz, hogy
kicsi x-ekre.
reMap nélküli eredmény (nagy, kicsi)
forrás (nagy, kicsi)
Az av_sym_oneway szimulációknál azonban más a helyzet. Itt a deformációt nem úgy választottuk meg, hogy a helyi feszültség 0-ra csökkenjen a deformációt követően, hanem úgy, hogy a deformáció értéke konstans 1 legyen, és csak az egyik irányban engedjük meg a megfolyást.
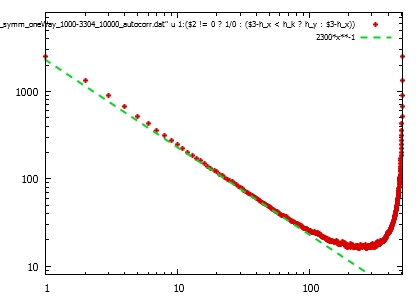
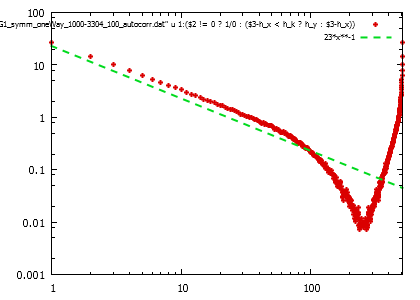
forrás (kicsi, nagy)


Lokális feszültség térkép nagy, illetve kicsi deformáicónál. Nagy deformációra jól közelíthető a görbe
összefüggéssel, azaz C=0. Érdekes a tört kitevő, mely reMap nélkül is jól látható. A térkép pozitív és negatív része.
forrás
Még érdekesebb, hogy kicsi deformációra lényegesen más a viselkedés, itt a tér autokorrelációja eleinte (a 0 pontot leszámítva) negatív, majd áttér pozitívba. A térkép pozitív és negatív része.
forrás