a=2 cellaméretű
Implementáltam az "a" paramétert a modellben, hogy Péter szimulációival összvethető eredményeket produkáljak.
Visszaadja-e Péter eredményeit?
A különbség Péter szimulációihoz képest, hogy
- a feszültségteret felösszegzett diszlokációkból, egzaktul vannak számolva
- densityInit = 1
- a folyáfeszültség eloszlásnek az átlaga 1, nem pedig a skálaparamétere
sysSize 64
a 2
densityInit 1
tau_b_coeff -0.4
tau_d_coeff 0.4
flowStressDistribution weibull_1.4_1.097185
gamma_final 1000000
maxStep 125000000
stressFieldKernelFname periodic_single_stress_field_symm128x128_bin.dat
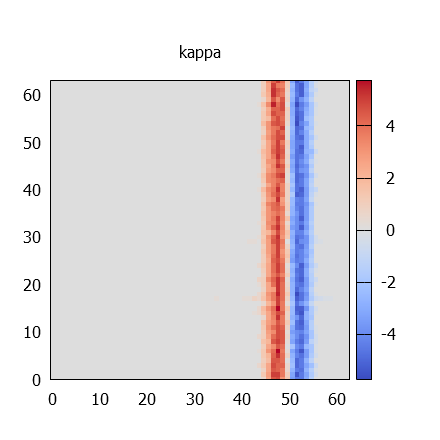
6-ból 3x teljesen egy falba rendeződtek a diszlokációk ennyi idő alatt
Kezdeti és végső értékek


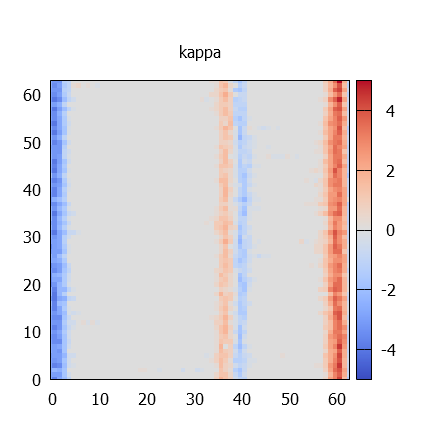
További 6 eset végső értéke
 t
tNagyobb rendszerméret
Vajon hogy függ a rendszermérettől a kialakuló mintázat?
sysSize 256
a 2
densityInit 1
tau_b_coeff -0.4
tau_d_coeff 0.4
flowStressDistribution weibull_1.4_1.097185
gamma_final 1000000
maxStep 125000000
stressFieldKernelFname periodic_single_stress_field_symm512x512_bin.dat
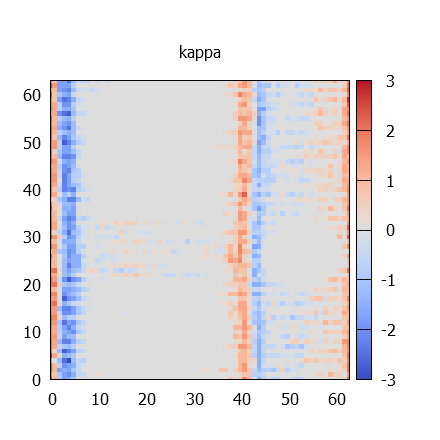
Kezdeti és végső értékek




További 6 eset végső értéke






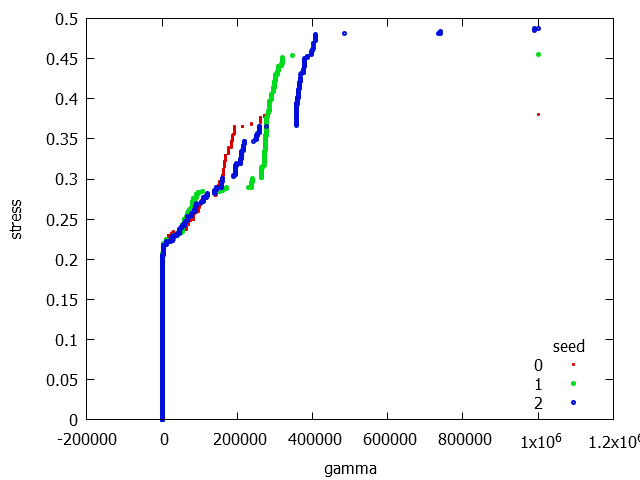
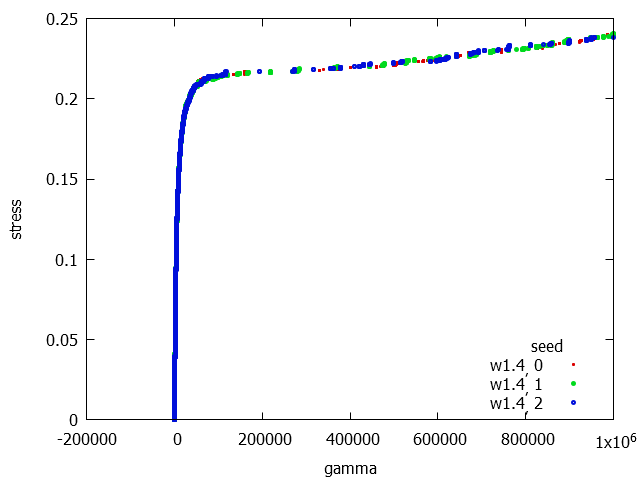
A feszültség-deformációs görbe azt sejteti, hogy ha tovább futtatnánk a szimulációt, látnánk még fejlődést.
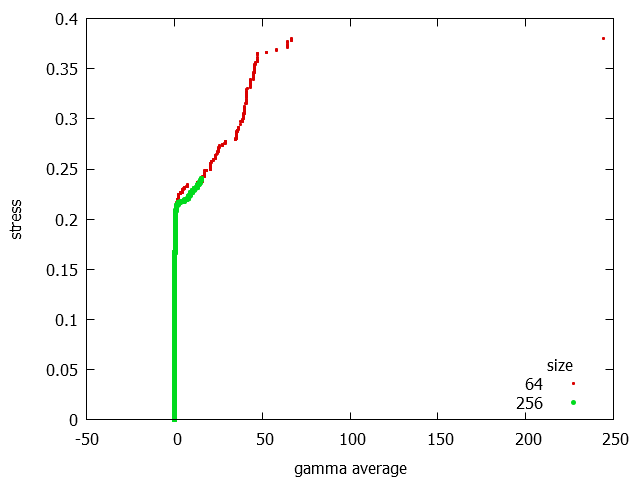
Ez még inkább látszik, ha összevetjük a kisebb rendszerméretű szimulációt a nagyobban.
Különböző flowStressDistribution használata
Készítettem Weibullból 1-es és 2-es alakparaméterű szimulációkat, illetve konstans 1 (0.9999 és 1.0001) értékűt.
sysSize 256
a 2
densityInit 1
tau_b_coeff -0.4
tau_d_coeff 0.4
- flowStressDistribution weibull_1.4_1.097185
fnamePrefix - flowStressDistribution uniform_0.9999_1.0001
fnamePrefix const_ys_ - flowStressDistribution weibull_1_1
fnamePrefix w1_
- flowStressDistribution weibull_2_1.12838
w2_
gamma_final 1000000
maxStep 125000000
stressFieldKernelFname periodic_single_stress_field_symm512x512_bin.dat
Az eredmények azt mutatják, hogy a lokalizáció mértéke nagyobb, ha az eloszlás szórása kisebb, de az eredmények amúgy elég hasonlók.









Különböző inicializáció és korrelációs integrál
Két különböző kezdeti inicializálás mellett megnéztem a lavinák kezdőpontjának a korrelációs integrálját, különböző külső feszültségek mellett.
- sysSize 256
- sysSize 64
a 2
- densityInit 0
fnamePrefix "w1.4_di0_" - densityInit 1
fnamePrefix "" vagy "w1.4_"
tau_b_coeff -0.4
tau_d_coeff 0.4
flowStressDistribution weibull_1.4_1.097185
gamma_final 1000000
maxStep 125000000
stressFieldKernelFname periodic_single_stress_field_symm512x512_bin.dat
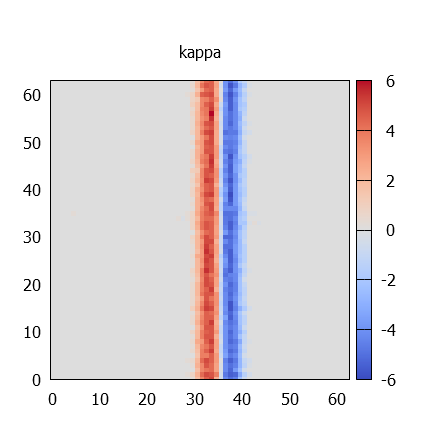
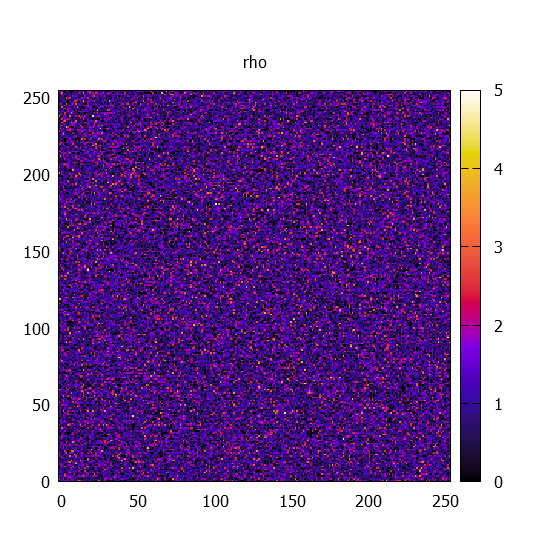
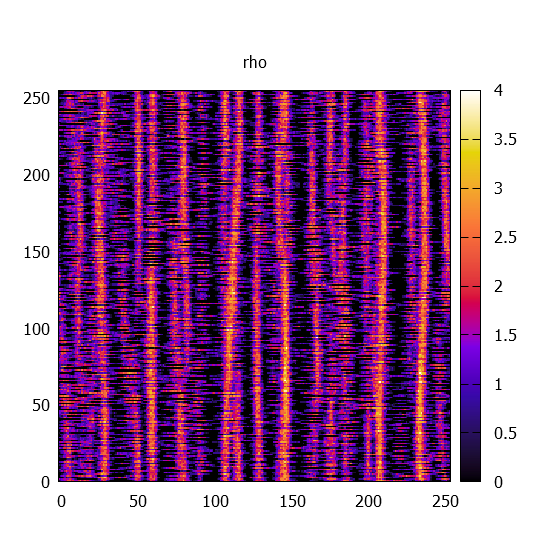
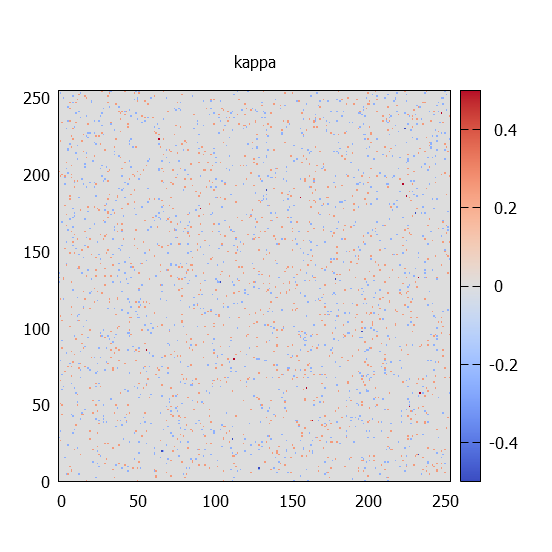
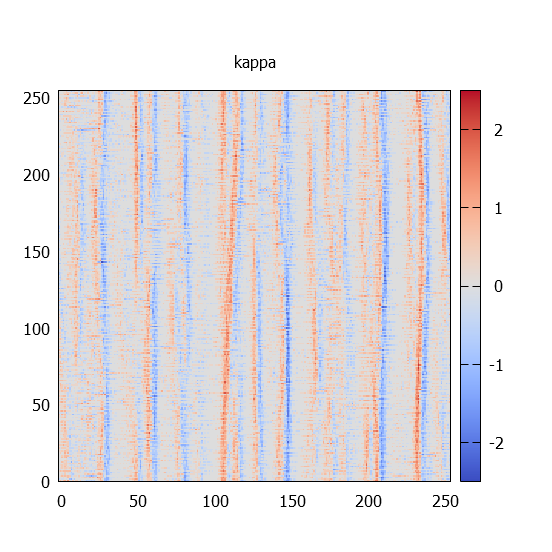
kappa térképek






korrelációs integrál, átlagos lavinaméret és feszültség-deformációs görbék
Egyes fesz-def görbék itt láhatóak. Alant van egy nagy kitálagolt is.
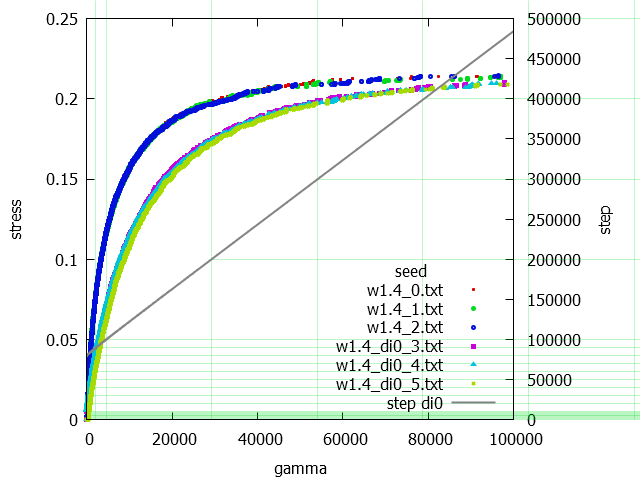
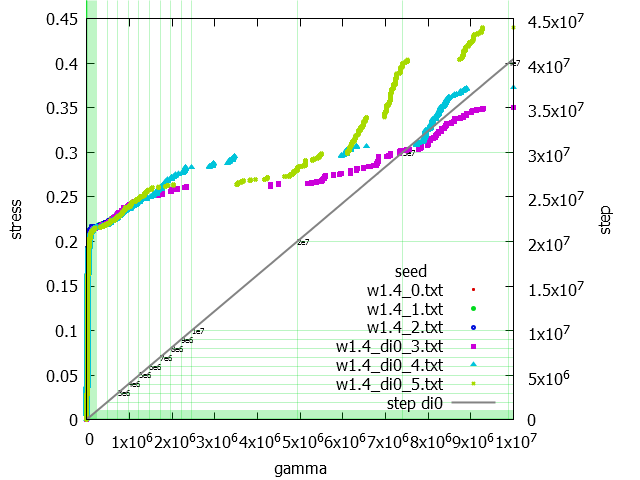
Ha kitátlagoljuk a fesz-def görbéket adott gamma értékeknél, az alábbit kapjuk.

A korrelációs integrált lehet vizsgálni különböző feszültség-tartományokban és különböző deformációs tartományban. A kezdeti feszültségintervallumokban sok esemény lesz, mert kicsik az események, és később sem olyan rossz a kép, mert elnyúlik a görbe. Viszont nagyobb feszültség értékeknél a görbe egy széles ívét adja vissza a korrelációs integrál.
A korrelációs integrál látható, hogy eltér 2-től mind a nagyobb feszültség, mind a nagyobb deformációs értékeknél.


Még csak 64-es és 256-os szimulációk vannak, ez utóbbiból csak 60 kb, ezért a statisztika még nem annyira jó. Futnak szimulációk a t1, t2 és t3 gépeken. (2016.11.22.)
